报告名称:A Hamiltonian Sufficient Condition for Completely Independent Spanning Trees
报告专家:郝荣霞
专家所在单位:北京交通大学
报告时间:2022年5月19日8:00
报告地点:腾讯会议(会议号:814 522 523)
专家简介:郝荣霞,北京交通大学, 教授, 博士生导师。曾获北京运筹学会青年优秀论文一等奖,校教学名师,智瑾奖教优秀教师,巾帼十杰等奖项,发表论文80余篇。主持和参加国家自然科学基金面上项目多项。参加国家自然科学基金重点项目1项。中国运筹学会图论组合分会第五届理事。国际期刊《International Journal of Computer Mathematics:Computer Systems Theory》编委,美国数学会《Mathematical Reviews》评论员。
报告摘要:Let G be a graph. Let
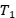 ,
,
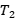 ,...,
,...,
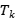 be spanning trees in G. If for any two vertices x and y in G, the paths between x and y in
be spanning trees in G. If for any two vertices x and y in G, the paths between x and y in ,
, ,...,
,..., are pairwise neither vertex nor edge in common, except x and y, then
are pairwise neither vertex nor edge in common, except x and y, then ,
, ,...,
,..., are called completely independent spanning trees in G. Com-
are called completely independent spanning trees in G. Com-
pletely independent spanning trees are powerful tools for reliable broad-casting and secure message distribution. In this talk, we prove the existence of dual-CISTs in G satisfying a Hamiltonian sufficient condition. Inaddition, we make a comparative analysis between the proposed condition and several known results on some graphs.
